How many times do they say bee in the bee movie

For some reason, people on youtube like to think of weird ways to watch the bee movie. case in point: “the whole bee movie, but every time it says bee, it speeds up by 15%.” (For a lengthy discussion of this general phenomenon, see the PBS Idea Channel video “The Bee Movie But Every Time They Say Bee We Explain The Bee Movie Deal”.)

In this post, I want to talk about something a little different: the fact that if you repeat the bee movie, but still follow the 15% faster rule every time they say bees, you end up causing a singularity where the movie goes through an infinite number of loops in finite time.

In the actual bee movie, the time from “bee” to “bee” varies. pedagogically speaking, that is an unnecessary complication. To understand how these kinds of systems behave, we’ll first focus on something simpler.

suppose we have a computer program that waits for 10 “ticks”, then prints the word “bee”, then speeds up what is a tick by 15%, and then repeats. if a tick initially lasts one second, how does this program behave?

well, at first 10 ticks is 10 seconds. so the program will sleep for 10 seconds, wake up and print “bee”. the next wait will also be 10 ticks, but the ticks will be $frac{1}{1.15} approx 0.87$ seconds due to the 15% speedup. so about 8.7 seconds later, the program will wake up and print its second “bee”. the third wait is again 15% faster, taking about 7.56 seconds.

15% speedups will continue to increase: 6.58 seconds, 5.72 seconds, 4.97 seconds, 4.32 seconds, and so on. clearly, the program will eventually end up printing “bee” at arbitrarily high rates.

To calculate when the nth “bee” should be printed, we can solve the power series that describes the backlogs:

$$sum_{k=0}^{n-1} 10text{s} cdot 1.15^{-k} = 10text{s} cdot frac{1 – 1, 15^{- n}}{1 – 1/1.15}$$

my god.

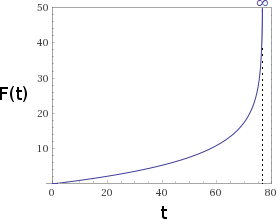
Do you see the numerator $1 – 1.15^{-n}$? goes up $n$ gets bigger, but it’s never going to be more than 1. so the time until $n$’th-“bee” is never going to be more than $10 text{s} cdot frac{ 1}{1-1/1.15} approx 76.6 text{s}$. the millionth “bee”, the “trillionth bee”, the graham number “bee”… after about a minute and a quarter, they will all be printed. there is a singularity.

we can see this very clearly by reversing our time-until-$n$’th-“bee” equation into a what’th-bee-at-time $f$:

function

$$t = 10 cdot frac{1 – 1.15^{-n}}{1 – 1/1.15}$$

$$n = -log_{1.15} left( 1 – frac{0.15}{11.5}t right)$$

$$f(t) approx. -7.16 ln(1 – 0.013t)$$

Do you see the problem? as $t$ increases, the natural logarithm argument will go down and down until it crosses 0. this causes a singularity, at $t approx 76.6$, where the output goes to infinity:

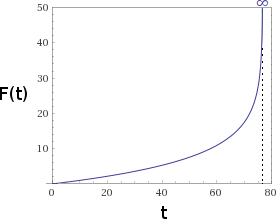
what does all this mean? means that our hypothetical program has to print an infinite number of “bees” in less than two minutes. clearly we’re going to need a faster computer!

Anyway, now we understand the general idea of ​​how these systems that make us go faster behave, including how often we get faster. Let’s apply that knowledge to the bee movie.

If we play the bee movie and make it 15% faster each time “bee” is uttered, it will transcend our mortal realm and graze the face of infinity. the question is: when? To answer that, we need data.

I went on the internet and found a subtitle file for the movie bee. this is how it starts:

after fighting the urge to roll my eyes at how incorrect that line is, I went through the file trying to get an idea of ​​what kind of “bee” strings appear. mostly there are a lot of “bees” and “bees”, some “bees” and “beekeepers”, and some words like “state” to avoid. in total, there seem to be 155 instances of a word “bee”:

Because I don’t hate myself, I didn’t use bash to parse the subtitle file to find out when each word “bee” occurs. I used python for that:

I then used python code to parse the subtitle file I downloaded:

Google says that the length of the bee movie is one hour and 35 minutes. Combine that with the timings we have on hand, and we can work out how long the first run of the movie will take:

just over 5 minutes. to be more precise: 5 minutes, 5 seconds, 633 milliseconds and change.

Because there are 155 “bee” words in the movie, the next execution will be $1.15^{155} approx 2.56 cdot 10^9$ times faster than the first. which means that the second cycle will finish in less than 3 microseconds. and the third cycle will finish in less than a femtosecond.

… yes.

Remember how the first loop went past 5:05.633? infinite loops will not reach 5:05.634. if you sat to the end of the first loop, chances are you accidentally sat to the end of all the loops. though it’s probably fine; Watching the bee movie infinitely many times in the span of a millisecond sounds perfectly normal and healthy.

There’s an infinitely long loop of movie to go through, but we’re off the end of the loop… what will play after that?

I’m pretty sure the video I linked isn’t combining accelerations correctly, because I didn’t transcend reality and achieve lighting while looking at the last frame.

discuss on reddit